|

  
|
||
Dake's recipe for evaluating vertical sweep efficiency in heterogeneous reservoirs is listed below.
"No matter what the nature of the vertical heterogeneity, the following recipe is applied to assess the sweep efficiency in edge waterdrive reservoirs.
| • | Divide the section in to N layers, each characterised by the following parameters: thickness, permeability, porosity, Swc, Sor, krw', kro'. |
| • | Decide whether there is vertical pressure communication (Vertical Equilibrium or VE) between the layers or not. |
| • | Decide upon the flooding order of the N layers and generate pseudo-relative permeabilities to reduce the description of the macroscopic displacement to one dimension. |
| • | Use the pseudos to generate a fractional flow relationship which is used in the Welge equation to calculate the oil recovery, Npd as a function of cumulative water influx, Wid. |
| • | Convert the oil volume to a fractional oil recovery, Np/N, and relate this to the surface watercut, fws." |
The Vertical Equilibrium (VE) condition means that the order in which the N selected layers flood is from the base layer to the top layer of the reservoir system. VE implies the dominance of gravity, however at no stage does a vertical gravity term appear in any of the displacement equations. Instead, all that is necessary is recognition of the fact that the water density is greater than the oil density, therefore water will naturally slump to the base of the reservoir and this dictates the flooding order of the selected layers.
If the selected layers are vertically isolated from one another, so that there is a total lack of cross-flow, then the order in which the layers flood out is determined by the actual velocity of the
frontal advance of water in each layer. See equation below.
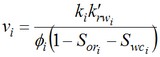
The dependence on permeability in the above equation is obvious. However concerning the terms in the denominator, low porosity rock, having a smaller capacity, will flood faster than high capacity, and similarly the smaller the movable saturation the more rapid the advance of water. The layers will therefore flood in decreasing sequence of their calculated values of velocity.
Having determined the flooding order of the layers the next step is to generate thickness averaged or pseudo-relative permeabilities across the section for edge waterdrive.
Four methods are provided to generate a fractional flow relationship, namely Heterogeneous and Homogeneous methods where there is vertical pressure communication between layers (Vertical Equilibrium or VE), and Stiles and Dykstra-Parsons methods where there is a complete lack of pressure communication between layers.
Once the fractional flow and Welge calculations have been performed, then the user can history match the field STOOIP value from a knowledge of the fields production and injection history, and finally can predict the future performance of the field via a knowledge of the production and injection constraints. This history matching and prediction performance is highlighted in more detail in the worked example.
Page url: http://www.YOURSERVER.com/help/index.html?introduction4.htm