Within the Waterdrive chapter of Dake's "The Practice of Reservoir Engineering", he presents a technique for examining and interpreting the waterdrive performance of reservoirs or numerical simulation models from inspection of their historic production/injection records. Extracts from this chapter as used to outline this technique.

 

"This approach to understanding the reservoir mechanics of a waterflood relies on the development of an underground fractional flow of water by solving the Welge equation in reverse. That is, for an observed set of production statistics: Np, Wi, fws, converted to their reservoir equivalents of Npd, Wid, fwe, the following equation is solved for Swe, thus establishing the fractional flow relationship: fwe versus Swe.

 

 

In this respect the reservoir or model, no matter how complex it may be: containing numerous vertical/horizontal wells, fractures or heterogeneity, is simply viewed as a Buckley-Leverett "black-box", in which the injection, qwi, and production, qo + qwp, are linked together by the fractional flow relationship."

 

The associated equations for Npd, Wid and fwe are included for completeness.

 

 

 

 

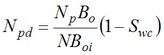
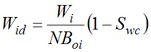
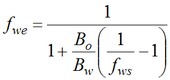
In solving the Welge equation for Swe, for values of Npd, Wid and fwe, it is assumed that the reservoir or simulator obeys Buckley-Leverett mechanics. Consequently, a fractional flow (fwe versus Swe) is obtained for which the extrapolation of the final points to the line fwe = 1 gives the value of Swbar, the average saturation in the "black-box", at that stage of the flood from which the oil recovery can be determined from :

 

 

and the reciprocal of the tangent of this extrapolation gives the cumulative water injection required to attain the recovery as :

 

 

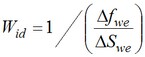
Linking the above two equations with the underground material balance for waterdrive under pressure maintenance conditions, included immediately below, allows the forward calculation of production and injection profiles for a given set of facilities constraints.

 

 

 

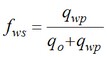
Integrating the above two equations, results in the following :

 

 

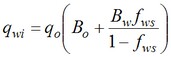
where,

qwi = water injection capacity

qo = oil processing capacity

qo + qwp = total separation capacity

qwp = water disposal capacity

 

The above techniques are outlined in more detail in the following example.

References:

Dake, L., "The Practice of Reservoir Engineering", Elsevier Scientific Publishing Company, 1994.

 

Welge, H.J., "Predicting Displacement Efficiency From Water-cut or Gas-Cut Field Data", SPE Paper 5313, 1975

 

Welge, H.J., "A Simplified Method for Computing Oil Recovery By Gas or Water Drive", Trans. AIME, 1952,

 

---

Page url: http://www.YOURSERVER.com/help/index.html?reverse_welge.htm